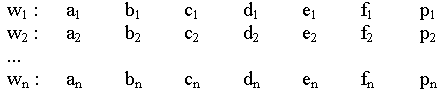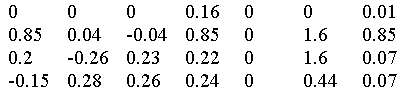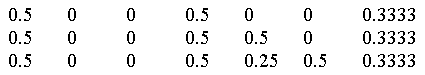Les IFS (Iterated Function Systems)
Avec le même principe que le jeu du chaos de Barnsley, on peut construire des fractales uniques en appliquant à un point une suite de transformations aléatoirement choisies dans un système de fonctions affines.
Définition
On se donne un espace métrique et un système d'applications contractantes qui sont des transformations affines du plan. Chaque transformation wn déplace un point Ai de coordonnées (xi,yi) vers un point Ai+1 (xi+1,yi+1) de la façon suivante :
wn : 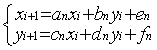 . Les coefficients an, bn, cn, dn, en, fn sont des constantes, ainsi que la probabilité pn associée à chaque transformation (on doit avoir
. Les coefficients an, bn, cn, dn, en, fn sont des constantes, ainsi que la probabilité pn associée à chaque transformation (on doit avoir 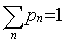 ). Une transformation affine est une combinaison d'une similitude et d'une translation. La transformation doit être contractante, c'est à dire que tous les points doivent être contenus dans un ensemble fermé.
). Une transformation affine est une combinaison d'une similitude et d'une translation. La transformation doit être contractante, c'est à dire que tous les points doivent être contenus dans un ensemble fermé.
Les n transformations d'une IFS sont contenues dans une matrice de n lignes et 7 colonnes, sous la forme :
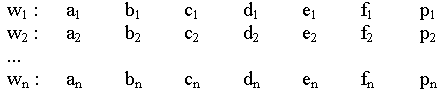
On retiendra que l'IFS est entièrement définie par cette matrice de 7n nombres.
Algorithme
C'est le même que celui du jeu du chaos de Barnsley, cependant les IFS laissent plus de liberté quant au choix des transformations.
On prend un point de départ dans le plan, par exemple (0,0). On lui applique une des transformation de l'IFS, prise au hasard selon son poids pn. On obtient ainsi un autre point du plan, auquel on applique une des transformation de l'IFS, et ainsi de suite. La suite de ces points est l'orbite du point de départ. On affiche tous les points sauf les premiers (qui ne feront pas partie de l'attracteur) et on obtient ainsi une représentation de l'attracteur. Celui-ci peut être fractal si les paramètres de l'IFS sont bien choisis.
Exemple de la fougère de Barnsley
C'est l'attracteur de l'IFS défini par :
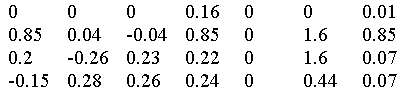
Voici deux fougères obtenues avec n itérations.
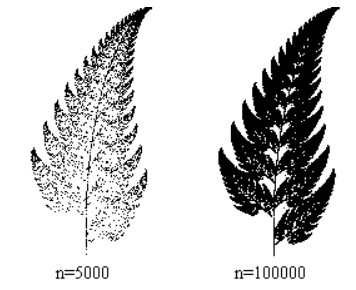
On peut tout d'abord s'étonner que les 28 nombres de la matrice d'IFS suffisent à créer une forme aussi "naturelle". Cependant, la spore à l'origine de la fougère ne contient qu'une quantité finie d'informations pour sa croissance. Il n'est donc pas étonnant, d'après Barnsley, que nous pouvions également trouver une petite quantité d'informations pour la décrire.
On peut encore retrouver le tamis (ou triangle) de Sierpinski :
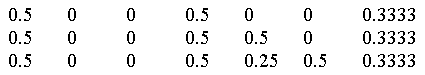
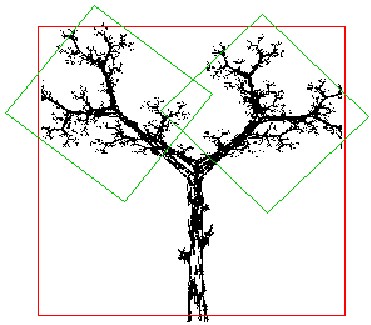
Il est également possible de retrouver la forme d'un arbre :
Nous avons trouvé l'attracteur connaissant l'IFS. Mais comment trouver l'IFS d'après une figure donnée ? On applique le théorème de collage, trouvé par Michael Barnsley.
En simplifiant, ce théorème propose d'appliquer à la figure entière (par exemple l'arbre ci-dessus) un polygone (le rectangle rouge), puis de placer des copies transformées (échelle, rotation...) de ce rectangle sur des parties de la figure afin de recouvrir toujours la même forme (rectangles verts). En calculant les transformation qui permettent de retrouver les rectangles vert à partir du rectangle rouge, on obtient les transformations de l'IFS.
On voit qu'un simple ensemble de règles, appliquées aléatoirement, permet de créer des formes fractales. La complexité de la forme obtenue est indépendante de la complexité des règles utilisées et de l'ordre d'application des ces règles.
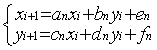 . Les coefficients an, bn, cn, dn, en, fn sont des constantes, ainsi que la probabilité pn associée à chaque transformation (on doit avoir
. Les coefficients an, bn, cn, dn, en, fn sont des constantes, ainsi que la probabilité pn associée à chaque transformation (on doit avoir